Shield AI

Planning for Real-time Blocking Flying Objects with a Redundant Manipulator

mentor: Ramkumar Natarajan, supervisor: Maxim Likhachev

Abstract

We consider the task of autonomously blocking flying objects for “robotcops” who are capable of guarding in cities. Such ability could be further applied to robots in partial-controlled scenarios, such as building sites, for self-protection. There already exist various algorithms which generate motion plans for high-dimensional manipulators. However, none of them can be applied in our domain due to two main challenges. As robots need to block objects in a short limited time, the motion planner is required to plan in real-time to get a time-optimal or suboptimal plan. In addition, as objects are often thrown from distance, robot’s perception system would gradually get better estimation when an object is getting closer. Consequently, the proposed planner should be able to adjust its motion plans when the estimation is updated. We present a new approach to meet those requirements by using offline auxiliary information. In simulation, We validate the performance of the proposed motion planner under different cases.

INTRODUCTION

In the modern times robots are expected to be deployed in unknown or complex scenarios to decrease workload and risk of human workers. The ability of self-protection is essential for robot in such real-world tasks since it prevents robots from damage to dramatically trim unnecessary cost of money and time. Such ability is also necessary for those robots which involve training in physical world since it prevents naive actions in early learning phase from hurting robot bodies. Existing work on robot self-protection focused on different aspects of the problem ranging from protecting fragile robot actuation [1], mechanical overload protection [2] and fall down protection [3]. However, using robot manipulator to block flying object, which is important for robot body protection, is still understudied. In this work, we consider the problem of motion planning for shielding off flying objects in a predefined surface in front of robots. Specifically, a robot will move an attached shield by its manipulator to a goal pose, which lies on a predefined surface, to block objects flying toward it.

To the best of our knowledge, there is no previous work on blocking object with manipulator. Although our task is similar with motion planning for reaching process of a pickup-object mission, the existing planners could be applied to our task directly. [4] use a kinodynamic motion planner to smoothly reach the moving objects. However, this planner cannot be used online while an object in flying imposes the requirement of short planning and reaching time. Apart from this, our problem can be modeled as a Moving Target Search problem as well. Existing approaches [5], [6] consider the case of heuristic search in 2D where an agent (hunter) is to catch a moving target (prey). Nevertheless, they are too computationally expensive to be applied to our task due to our high-dimensional property. [7] presented an efficient CNN architecture for real-time manipulator grasping. How ever, such learning approach is expensive to be implemented when various shields are attached.

The shielding process highly relies on quality detection and localization of flying objects since we use the object’s pose to compute its landing pose, namely our goal state, in the predefined surface. Unfortunately, the initial perception estimates of the object’s pose are inevitably inaccurate due to perception noise. What is worse, as the object is far from robot initially, a slight error of the object’s pose will lead to a large error for its landing pose. A proper filter can help to reduce the detection error gradually. Thus, the landing point estimation becomes fairly accurate only if the object moves closer as well as the filter error decreases. However, if the robot waits too long to get an accurate estimate, the delay in starting plan execution could cause the shield to miss the object. The robot therefore should start executing a plan computed for the initial goal pose. In addition, when the robot gets better estimation for the goal states, it should repeatedly replan for the new goals. For every replanning query, the time window for shielding shrinks. This makes the time for each planning step even less. Since planning problem is high-dimensional and requires collision avoidance as well, it’s infeasible to purely plan online. [8] proposed a planner that leverages offline preprocessing to provide bounds on the planning time when the planner is invoked online. However, this approach relies on the assumption that there’s a replan cutoff time. In our task, the time for a object to hit the surface depends on the initial pose and velocity of the object. Consequently, for every case the robot should reach its goal state as soon as possible and we cannot assume a fixed cutoff time for it. This suggests the experience compressing technique in [8] cannot be applied directly in our task. And, there is no planner satisfies our specific task.

In this work, we only consider the real-time challenge of planning and blocking. Our planning algorithm based on a provable real-time planner [9] that leverages compressed offline experience for only blocking. This real-time planner is used in pre-processing phase to compute and store important paths to so-called ”attractors”. An attractor is matched to a ”subregions” where we can find a collision-free path from any state inside to the attractor by greedy search. We finely define the problem and present how to apply this planner to a goal region that the shield is on a curved surface. We complete the query algorithm that finds goal states and generates motion plans by combining the pre-computed path from initial state to the attractor and greedy path from attractor to goal state. The effectiveness of our algorithm is demonstrated in simulation on a PR2 robot.

PROBLEM DEFINITION

The task presented in this paper is to generate collision-free motion plans for a robot to block objects flying toward it for self-protection. We define the world state W to be comprised of a robot, an attached shield and an object O. The shield is a cylinder with negligible height $h_s$ and a radius $r_s$. At every point of time, there is at most one object in the scene attacking the front side of the robot. The pose of the object $g_o$ are detected by robot’s perception system.

Our planner P takes \(g_o\) as input. If O is going to hit the robot body, its landing pose \(g_l=[p_l, v_l]\), at which O will land on a predefined surface, will be determined. Then P will output a collision-free motion plan for the robot’s manipulator R to move to a valid goal configuration \(s_{goal}\) for defense. In fact, the robot can use its shield to block an object at different positions and orientations thanks to the shield’s area. Namely, at \(s_{goal}\), the position of the shield \(p_s\) can be slightly deviated from \(p_l\) and the normal vector of shield surface \(v_s\) can be slightly unparalleled to \(v_l\) as long as they guarantee successful blocking. Hence, given an \(g\), P probably generates a set of goal configurations. It will try them out until successfully query a plan for R to execute. Apart from this, we assume R starts from an fixed initial configuration $s_{home}$ in each blocking process. \(s_{home}\) is a predefined configuration where R can reach any \(s_{goal}\) in goal region G within a relatively fixed and small amount of time. We emphasize that all poses in this paper are represented in robot’s body frame, which can be directly measured by attached sensors.

A. Surface Definition

The surface should be defined to offer sufficient protection to the front of the robot. Compared to a plane, a curved surface is more reasonable to be adopted. Further considering the simplicity, we define the surface as a spherical cap. \(\begin{equation} \label{spherical} \left \{\begin{matrix} (x-x_{org})^2+(y-y_{org})^2+(z-z_{org})^2=r^2 \\ Angle((x-x_{org},y-y_{org},z-z_{org}),(1,0,0))<\alpha \end{matrix}\right. \end{equation}\) Where x axis is positive forward and negative backward while z axis is positive upward and negative downward. Typically \(x_{org}<0\), \(y_{org}=0\) and \(z_{org}=\frac{h_{robot}}{2}\).

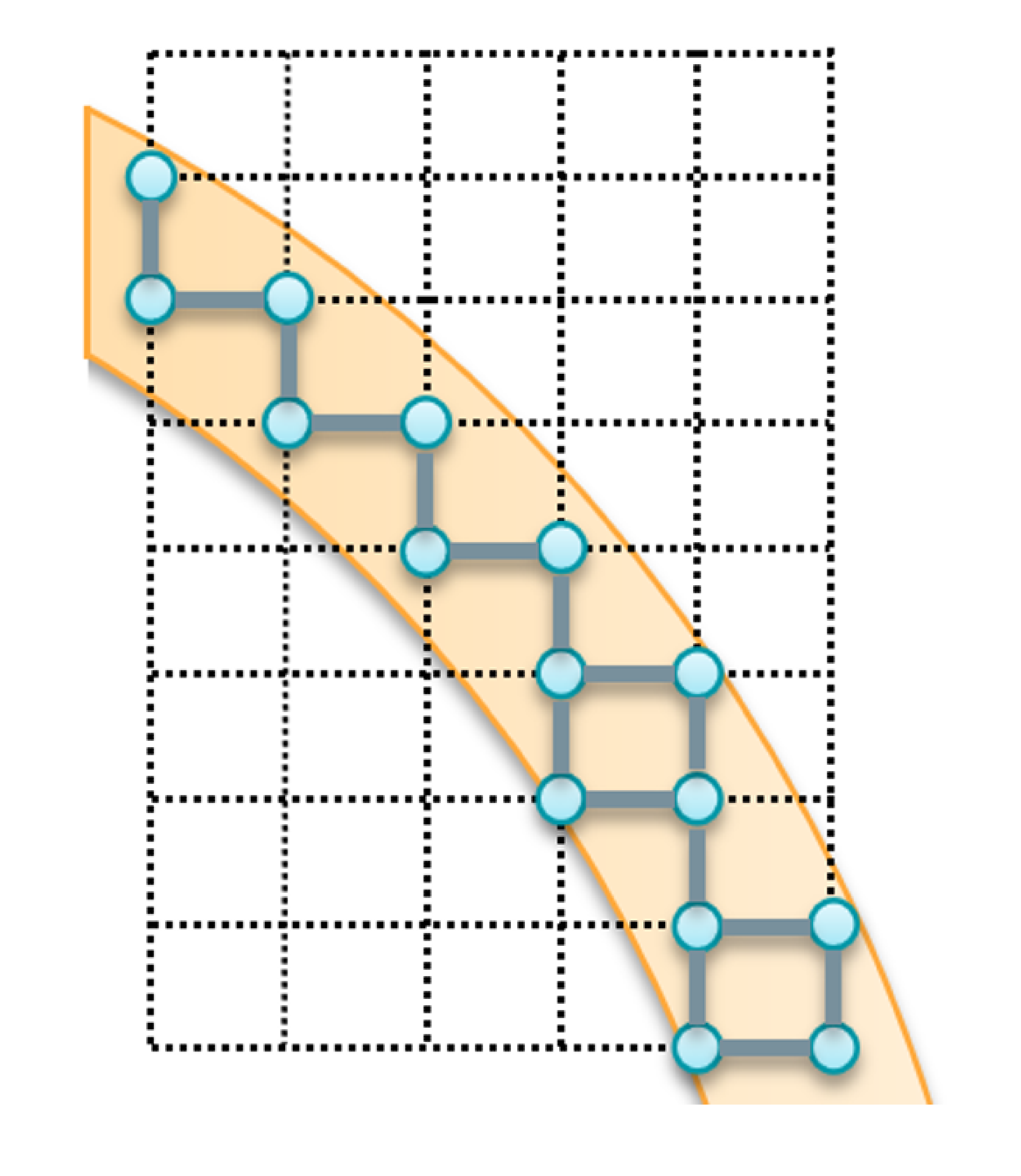
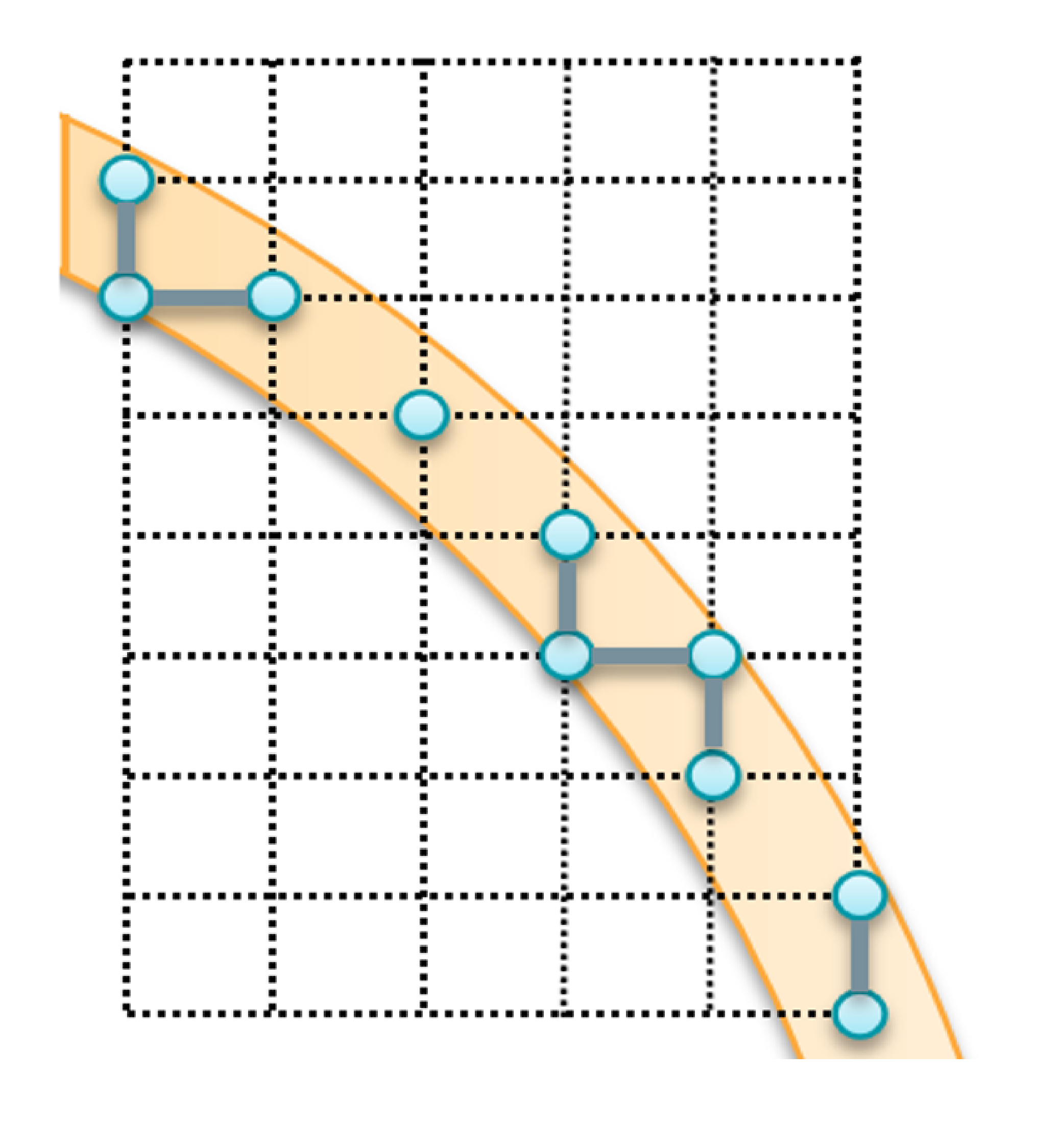
_{The orange region is a cross section of the surface. Each blue dot in the figure represents several goal configurations of \(**R}\) where shield’s positions are the same with dot’s position in the cross section and shield’s orientations are different. Blue lines state if there are any two configurations in two blue dots connected. (a) When \(\epsilon<\frac{\sqrt{2}\Delta_{max}}{2}\), we cannot implicitly build the graph of goal region since the graph of goal region is not connected. (b) When \(\epsilon>\frac{\sqrt{2}\Delta_{max}}{2}\), the graph of goal region is guaranteed to be strong connected.}

B. Goal Region Definition

We discretize the manipulator’s configuration space C into a state lattice S. In addition, each state is connected to its successors and predecessors by a set of motion primitives. The motion planning problem can therefore be transferred to a graph search problem. That is, the planner can search a path between two states on the graph for motion planning. However, the constructed graph may not be strong connected due to the curved surface setting, which means we may not find a path from one state to another, unless we enlarge G to be the set of \(s_{goal}\) at which distance between shield position and the surface is under a threshold \(\epsilon >\frac{\sqrt{2}\Delta_{max}}{2})\), where \(\Delta_{max}\) is the maximum displacement of motion primitives (see the figure above). The region of shield’s goal positions is actually several discrete rings on different planes. Lastly, the set of \(s_{goal}\) within C is denoted by \(G_S=C \cap G\)

METHOD

A provably indefinite-horizon real-time planning algorithm was proposed in [9]. Based on the same thought of path compression mechanism, our algorithm framework includes an offline preprocessing phase and an online object-blocking phase. The planner generates paths to the goal region and stores them in computer memory in the preprocessing phase while queries paths from memory to speedup planning process in the object-blocking phase.

A. Preprocessing Phase

We employ the preprocessing algorithm, which is presented in details in \cite{islam2019provable}. The preprocessing phase takes as input the initial configuration \(s_{home}\), the surface definition and a conventional motion planner, and outputs a set of subregions and the corresponding library of paths from \(s_{home}\) to each \(s_{attractor}^i\). Before explaining the algorithm, we introduce two definitions.

• A configuration is valid if the manipulator does not collide with itself and the robot body under this configuration.
• A configuration is invalid if the manipulator collides with itself or the robot body under this configuration.

The algorithm maintains a set of frontier valid states \(V\) and a set of frontier invalid states \(I\) to help finding uncovered valid states and invalid states, respectively. Both \(V\) and \(I\) are empty at the beginning. The preprocessing phase initiates with sampling a state in \(G_S\) and push it into \(V\). Then it covers the whole \(G_S\) with subregions by repeating following pipeline until both \(V\) and \(I\) get empty.

• Find a state \(s\) not covered by any subregion as \(i^{th}\) attractor \(s_{attractor}^i\):
  • If \(V\) is not empty, repeatedly pop the first state from \(V\) until the state \(s\) is uncovered yet. Set \(s\) as \(s_{attractor}^i\).
  • Otherwise, “go through” invalid regions to find a uncovered valid state and push it into V. Then jump to the next round.
• Compute a hyperball subregion \(G_i\) center at \(s_{attractor}^i\) with a radius \(r_i\) by the algorithm \(ReachabilitySearch\) to cover surrounding states.
• Generate a path \(\Pi_i\) for \boldsymbol{R} to reach the \(s_{attractor}^i\) from \(s_{home}\). Store the path, attractor number and the subregion’s radius.
• Get corresponding frontier states, which are just outside \(G_i\), and push them into V and I according to whether valid or not.

When the iteration stops, all attractors with their corresponding paths and radius are stored in computer memory. Some further explanation may help understanding the algorithm. When we “go through” invalid regions, invalid states will be popped out after checking in order to make sure \(I\) ends up to be empty. \(G_i\) includes and only includes states that have a heuristic value \(h(s, s_{attractor}^i)<r_i\). A collision free path from any state to the attractor of its subregion can be found by a simple greedy search.

B. Object-Blocking Phase

In Object-blocking phase, the robot keeps sensing the environment. When a new object is detected, the algorithm calls the procedure \(BlockObject\) once. The precedure takes \(g_o=[p_o,v_o]\) as input. It starts by predicting \(g_l\) and produce a stack of manipulator’s goal configurations \(G_s\) that contains multiple choices for blocking. Poping the first \(s_{goal}\) from \(G_s\), it then finds an attractor to which the heuristic value of goal configuration \(h(s_{goal}, s_{attractor}^i)<r_i\). If there is no such attractor or \(s_{goal}\) is invalid, the planner will recover by popping next \(s_{goal}\) to query unless the stack gets empty. After getting the corresponding attractor \(s_{attractor}^i\), a greedy search is employed to give the path from \(s_{goal}\) to \(s_{attractor}^i\). We reverse the greedy path and append it into the pre-computed path \(\pi_i\) to get the completed path for R to execute.

B.1 Goal state prediction

In this preliminary work, the object is modeled as a mass point without any aerodynamics characteristics. Hence, the its trajectory is a parabola \(\begin{equation} \left \{\begin{matrix} x=x_0+v_xt \\ y=y_0+v_yt \\ z=z_0+v_zt-\frac{gt^2}{2} \\ \end{matrix}\right. \end{equation}\) Combine the trajectory with the surface representation (\ref{spherical}), we get a quartic equation of t \(\begin{equation} at^4+bt^3+ct^2+dt+e=r^2 \end{equation}\) where \(\begin{equation} \begin{aligned} & \quad a=\frac{1}{4}g^2 \\ & \quad b=-gv_z \\ & \quad c=v_x^2+v_y^2+v_z^2-gz_0+z_{org}g \\ & \quad d=2(x_0v_x-x_{org}v_x+y_0v_y-y_{org}v_y+z_0v_z-z_{org}v_z) \\ & \quad e=(x_0-x_{org})^2+(y_0-y_{org})^2+(z_0-z_{org})^2 \nonumber \end{aligned} \end{equation}\) We apply Ferrari’s method to solve the equation. We take the minimum real root as object’s landing time and use it to compute $g_o$. The object will not hit the surface if there is no real root or \(\begin{equation} Angle((x_l-x_{org},y_l-y_{org},z_l-z_{org}),(1,0,0))>\alpha \end{equation}\) To generate \(G_c\), we compute all possible poses of the shield, solve their inverse kinematics and push them into \(G_c\). Specifically, we first find the best shield pose, then we find all shield poses having same position and similar orientation (\(\delta_{roll}<\epsilon_{roll},\delta_{yaw}<\epsilon_{yaw},\delta_{pitch}<\epsilon_{pitch}\)) and push their configurations into \(G_c\). The best position is the same with \(p_l\). The best shield orientation is defined to be opposite to \(v_l\), namely the shield surface is perpendicular to \(v_l\).

C. Detail Adjustment

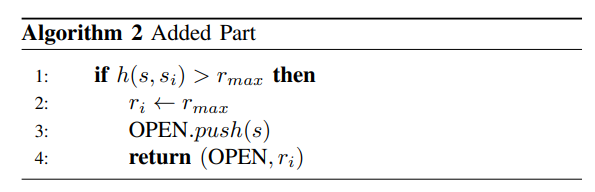
As a whole motion plan is composed of a path from initial state to the attractor and a path from the attractor to goal state, it is a sub-optimal solution. What’s more, the longer the second path is, the longer the extra execution time will be. We therefore restrict the radius of subregions with a maximum value \(r_{max}\) by adding pseudo code between line 7 and 8 in procedure ComputeReachability

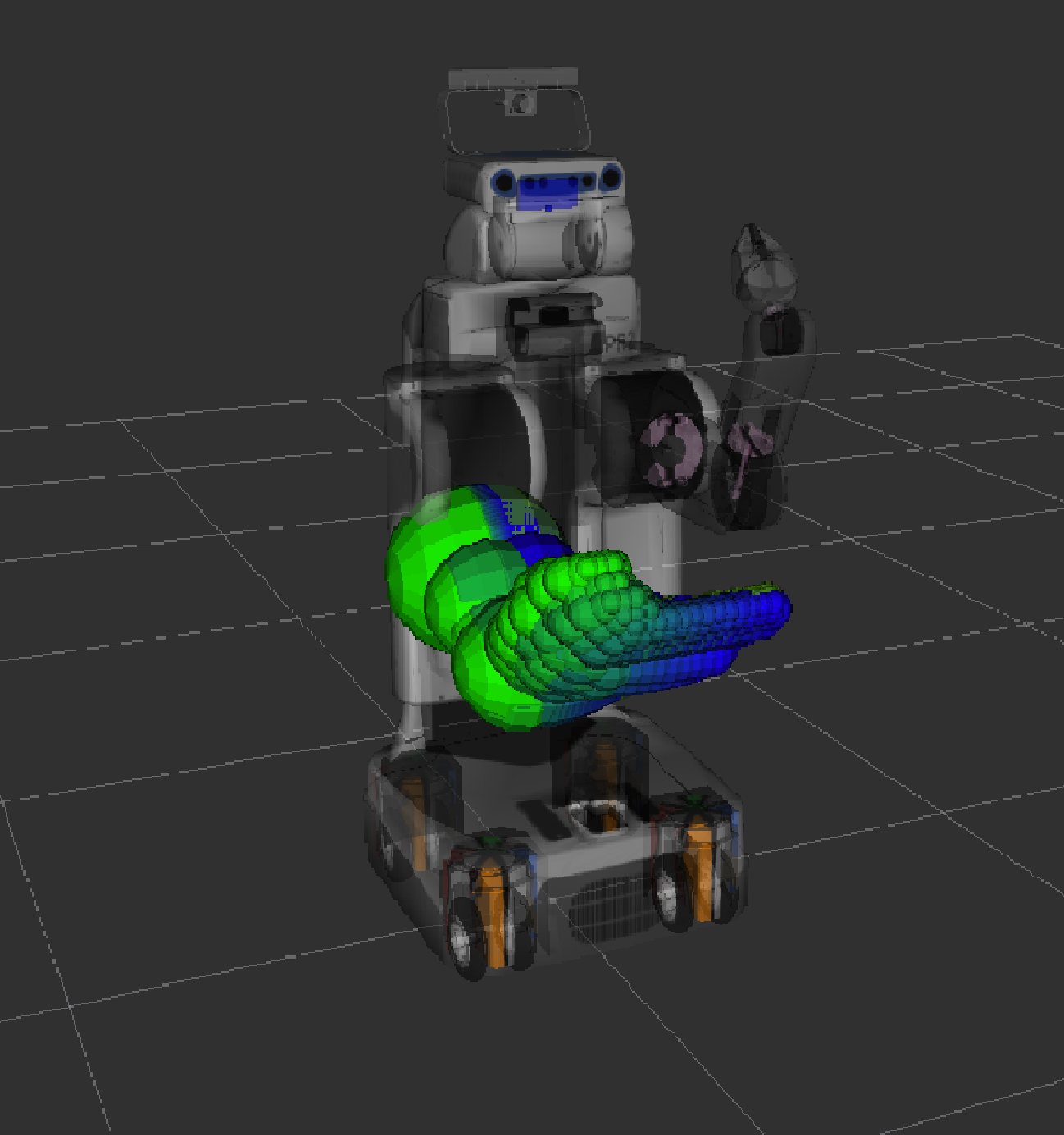
_{When the radius of a subregion is too large, the greedy path (b) may be large compared to the pre-computed path (a), which means the path is far not optimal.}

SIMULATION

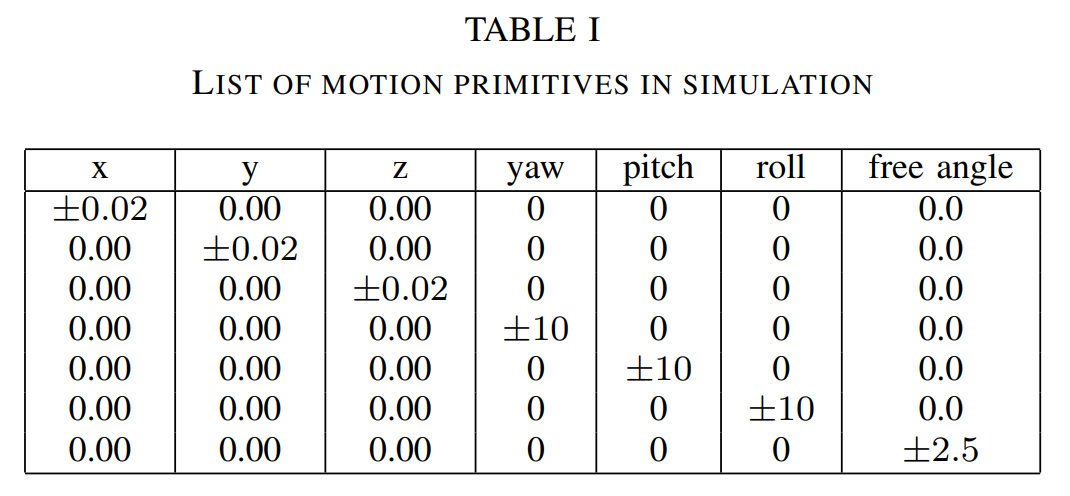
We performed simulations on PR2 robot to evaluate our algorithm. The algorithm and simulation environment are implemented using C++ on ROS. An Intel Core i7-7700HQ 2.80GHz CPU machine is employed for simulation. We discretize our graph with a resolution of 2cm in position axes, 10 degrees in Euler axes and 2.5 degrees for the redundant joint. The primitives are defined as subtle movements of the shield in position axes (x, y, z) and orientation axes of Euler angles (roll, pitch, yaw) and subtle movements of the redundant joint (shown in Table1). To be clear, the deviation between poses of the shield under a state and its predecessor/successor is one of the motion primitives. The heuristic function is the Euclidean distance in joint space and the maximum radius of subregion is 0.06. We design the shield to have a radius of 8cm and negligible inertia in Solidworks. For all tests, the surface are defined as : \(\begin{equation} \left \{\begin{matrix} (x-0.7)^2+(y-0)^2+(z-0.9)^2={1.56}^2 \\ Angle((x-0.7,y-0,z-0.9),(1,0,0))<0.4 \end{matrix}\right. \end{equation}\)

It’s notably that we assume our perception system to be perfect so that we can start planning right after an object shows up. That is, the distance between the robot and object’s initial position, which affects accuracy of perception, can be fixed in our simulation. To further reduce the workload, we only plan for the right arm to block the right part of the surface, which obviously will not lead to any impact on results. We evaluate how optimal the overall path is by the ratio between extra path length and total path length. Also, We take number of subregions, planning execution time, query time and search time as other assessment indexes.

We generate 200 random tests for each setting. In each test, an object is initially placed randomly on an arc centered at the PR2 robot with a radius of 8m and a radian of \(\alpha\). Its velocity is randomly sampled within a range. The key idea is to make sure its possible landing poses cover the whole predefined surface. Specifically, we first randomly pick a position on the arc and let the object flies directly to PR2 robot with a random speed in xy plane from 3m/s to 8m/s. Then we randomly generate a pitch angle from -50 degrees to 50 degrees and height from 0.4m to 1.6m for the object to land on. Lastly, the initial height and velocity along z-axis are determined by simulate the movement backward. The preprocessing takes about two hours and there are in total 6534 subregions. We present the results under different initial poses of the shield in Table2. The succesful rate of planning is \(100\%\).

CONCLUSIONS

In this work, we have presented a preprocessing-based kinodynamic motion planning algorithm that generates collision free trajectories for a manipulator to block flying objects. We build our algorithm on a provable real-time planning algorithm to deal with the high dimensionality and time restraint of our task. We conduct simulation on PR2 robot to show that our algorithm is capable of planning an acceptable path within a short time window. In future work, we will consider uncertainty in the perception system, which involves replanning problem. And we will setup real-world experiment for evaluation.

REFERENCES

[1] G. Walck, R. Haschke, M. Meier, and H. J. Ritter, “Robot self-protection by virtual actuator fatigue: Application to tendon-driven dexterous hands during grasping,” in 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2017, pp. 2200–2205.

[2] T. Yoshikai, M. Hayashi, A. Kadowaki, T. Goto, and M. Inaba, “Design and development of a humanoid with soft 3d-deformable sensor flesh and automatic recoverable mechanical overload protection mechanism,” in 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE, 2009, pp. 4977–4983.

[3] M. Hayashi, R. Ueda, T. Yoshikai, and M. Inaba, “A fall down resistant humanoid robot with soft cover and automatically recoverable mechan ical overload protection,” in Advances In Mobile Robotics. World Scientific, 2008, pp. 1225–1232.

[4] A. Cowley, B. Cohen, W. Marshall, C. J. Taylor, and M. Likhachev, “Perception and motion planning for pick-and-place of dynamic ob jects,” in 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE, 2013, pp. 816–823.

[5] T. Ishida and R. E. Korf, “Moving target search.” in IJCAI, vol. 91, 1991, pp. 204–210.

[6] S. Koenig, M. Likhachev, and X. Sun, “Speeding up moving-target search,” in Proceedings of the 6th international joint conference on Autonomous agents and multiagent systems, 2007, pp. 1–8.

[7] U. Asif, J. Tang, and S. Harrer, “Graspnet: An efficient convolutional neural network for real-time grasp detection for low-powered devices.” in IJCAI, 2018, pp. 4875–4882.

[8] F. Islam, O. Salzman, A. Agraval, and M. Likhachev, “Provably constant-time planning and re-planning for real-time grasping objects off a conveyor,” arXiv preprint arXiv:2003.08517, 2020.

[9] F. Islam, O. Salzman, and M. Likhachev, “Provable indefinite-horizon real-time planning for repetitive tasks,” in Proceedings of the International Conference on Automated Planning and Scheduling, vol. 29, no. 1, 2019, pp. 716–724.