Convex Optimization Ch.1
Introduction
This blog series aims to provide a clear, yet conprehensive note about convex optization based on the ESE 605 course material at UPenn. The goal is that after reading this blog, the readers would be able to
- recognize and formulate problems as convex optimization problems
- develop code for problems of moderate size
- characterize optimal solution, give limits of performance, etc.
The following topics are included
- convex sets, functions, optimization problems
- examples and applications
- algorithms
Canonical form of convex optimization
$$\begin{array}{ll} \operatorname{minimize} \ f_0(x) \\ \text { subject to } f_i(x) \leq b_i, \quad i=1, \ldots, m \end{array}$$
-
where objective and constraint functions are convex $$ \newline f_i(\alpha x+\beta y)\leq \alpha f_i(X)+\beta f_i(y)) $$
if \(\alpha+\beta=1,\alpha\geq 0, \beta \geq 0\)
Convex sets
For the following definitions, click to expand
Lines 👇
all points through x1, x2$$\{x \mid x=\theta x_1+(1-\theta) x_2 , \ \theta \in \mathcal{R} \}$$
Affine set 👇
contains the line through any two distinct points in the set.Every affine set can be expressed as solution set of system of linear equations example : solution set of linear equations $$\{x \mid A x=b\}$$
Line segment 👇
all points between x1, x2$$\{x \mid x=\theta x_1+(1-\theta) x_2 , \ \theta \in [0,1] \}$$
Convex set 👇
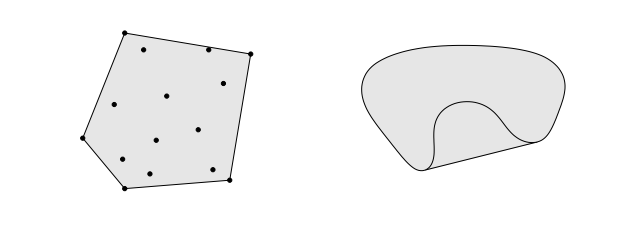
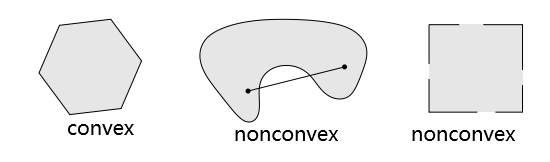
contains line segment between any two points in the set$$x_1, x_2 \in C, \quad 0 \leq \theta \leq 1 \quad \Longrightarrow \quad \theta x_1+(1-\theta) x_2 \in C$$ Examples:
A convex set can be represented by convex combination
Convex combination and convex hull 👇
convex combination of x1, ..., xk includes any point x of the form$$x=\theta_1 x_1+\theta_2 x_2+\cdots+\theta_k x_k$$
with $$\theta_1+\cdots+\theta_k=1, \theta_i \geq 0$$convex hull conv(S) is the set of all convex combinations of points in S